去年1月，教育部发布《普通高中课程方案和各科课程标准（2017年版）》，此次课程标准的修订力度较大，并首次提出凝练“学科核心素养”。可以预见，对学科核心素养的考查，将是2018年乃至今后高考的重要内容。

那么，高考数学核心素养是什么？它们在高考试题中怎样呈现和考查？对复习备考有哪些要求？2018年高考命题可能会怎样体现？需要考生关注的重点是什么？

数学核心素养是什么？

数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。共六项三大类。

（数学抽象与直观想象体现了数学的一般特性。）

（逻辑推理与数学运算体现了数学思维的严谨性。）

（数学建模与数据分析体现了数学的实用性。）

数学核心素养怎么考？

1.通过由具体的实例概括一般性结论，看学生能否在综合的情境中学会抽象出数学问题，并在得到数学结论的基础上形成新的命题，以此考查数学抽象素养。

2.通过提出问题和论证命题的过程，看学生能否选择合适的论证方法和途径予以证明，并能用准确、严谨的数学语言表述论证过程，以此考查逻辑推理素养。

3.通过实际应用问题的处理，看学生是否能够运用数学语言，清晰、准确地表达数学建模的过程和结果，以此考查数学建模素养。

4.通过空间图形与平面图形的观察以及图形与数量关系的分析，通过想象对复杂的数学问题进行直观表达，看学生能否运用图形和空间想象思考问题，感悟事物的本质，形成解决问题的思路，以此考查直观想象素养。

5.通过各类数学问题特别是综合性问题的处理，看学生能否做到明确运算对象，分析运算条件，选择运算法则，把握运算方向，设计运算程序，获取运算结果，以此考查数学运算素养。

6.通过对概率与统计问题中大量数据的分析和加工，看学生能否获得数据提供的信息及其所呈现的规律，进而分析随机现象的本质特征，发现随机现象的统计规律，以此考查数据分析素养。

例如，在2017年高考中，全国II卷第20题第（1）问以椭圆的标准方程为依托，设计了线段之间的相量关系式等条件，考查求动点轨迹的方法；第（2）问设计了动直线相互垂直的证明问题，重点考查思维的灵活性以及综合应用知识解决问题的能力。

全国III卷第8题考查圆柱和球的相关概念，以此考查考生的空间想象能力、逻辑推理能力和运算求解能力。

北京卷第14题通过图表给出信息，考查了考生的数据处理能力和逻辑推理能力。

上海卷第12题以点与线的位置关系为背景，考查了空间想象能力、逻辑推理能力，突出考查数学的理性思维。

2018年：数学核心素养怎么练？

1.要重视基本概念的复习

从概念的定义出发，由表及里，去伪存真，掌握概念的本质属性，这是提升数学素养的必要条件。

例1：命题：“若（X-1）（X+2）=0，则X=1”的否定是____。

很多人认为命题的否定就是否定命题的结论，所以“若P则Q”的否定就是“若P则?Q”，其实这种理解是错误的。如果按照这种理解，上述命题的否定就是“若（X-1）（X+2）=0，则X≠1”，这个结果显然是错误的，因为这个命题与原命题都是假命题。

我们来看看教材中“命题的否定”的定义：

人教A版：对一个命题P全盘否定，就得到一个新的命题，记作?P，读作“非P”或“P的否定”。

人教B版：对命题P加以否定，就得到一个新的命题，记作?P，读作“非P”或“P的否定”。

根据上述定义及符号语言可以看出，命题的否定是对整个命题的否定，而非只对其结论进行否定。因此这个命题的否定就应该是“并非对（X∈R，若（X-1）（X+2）=0，则X=1”，也即“存在X∈R，使（X-1）（X+2）=0，且X≠1”。

此外，在概念复习中还要避免模式化，避免机械套用有关结论。

2.要重视基本定理、公式的复习

很多学生存在重应用轻推导的现象，就是只重视定理公式的应用，而忽视公式的推导、定理的证明。事实上，重视公式的推导、定理的证明，不仅有利于理解与掌握定理和公式，理解公式之间的相互关系，而且还可以进一步挖掘公式中蕴含的数学思想，从而成为我们解决有关问题的敲门砖。

比如点到直线距离公式的教学，包括教科书在内基本上都舍弃了解析法，即“求出过点P与直线L垂直的直线PQ的方程，然后求出点Q的坐标，最后利用两点间距离公式求出PQ的长”的方法，普遍认为上述方法虽然思路自然，但具体运算需要一定技巧。

其实利用上述方法，运算量并不是大到不可接受，如果方法得当，学生一定对解析法印象深刻，并会在有关问题中应用解析法解决问题。这也正体现了解析几何的本质，即利用代数方法（方程、坐标）解决几何（曲线）的有关问题。

3.要重视基本技能的复习

基本技能是数学基础知识的重要组成部分，在数学建模、数学运算以及数据分析等核心素养中都有它的影子，也是历年高考考查的重点。对基本技能的复习，主要包括掌握入手点、了解隐藏点与熟悉易错点。

所谓掌握入手点，就是要掌握基本思想方法，通过分析其本质特征，熟练掌握其适应范围，掌握基本问题的基本解法。

所谓了解隐藏点，就是要了解哪些知识有隐藏的漏洞，必须与哪些知识配合使用才能避免产生错误。如在解析几何中解决直线与圆锥曲线相交的问题时，如果使用了韦达定理，就必须检验判别式是否大于零，否则就可能出现直线与圆锥曲线没有交点的情况。

所谓熟悉易错点，如忽略函数的定义域、数列中没有注意N的取值范围等问题而导致错误。这些虽然不难掌握，但是如果不注意很容易出现错误。这也体现了数学核心素养中逻辑推理的严谨性。

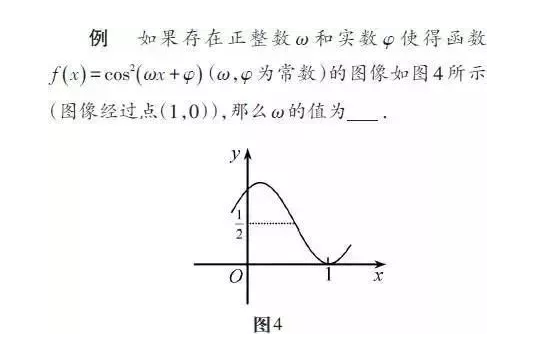
设问1：如何求未知数Ω的值？（设法得到关于Ω的方程）

设问2：两个未知数需要两个方程才可能求出它们的值，而此题我们只能得到一个方程，怎么办？

设问3：注意到Ω是正整数，因而通过范围就可以求出其值，那么如何能得到关于Ω的不等式呢？

通过以上设问，应该容易想到通过函数的图像可以得到关于周期的不等式，从而得到关于Ω的不等式，问题得以解决。

这就是把数学思想与核心素养相结合的一个很好的例子，以此培养能力，效果一定不错。

4.要重视数学本质

数学核心素养中的数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征，贯穿在数学知识的产生、发展、应用的全过程中。

导数既是函数的一个重要概念，同时也是研究函数性质，解决函数有关问题的一个重要工具。复习中不仅仅要重视导数的概念、运算以及应用，还要突出导数的工具性，突出导数在研究函数的有关性质、解决函数有关问题时的工具作用。

有人会觉得此题有超纲的嫌疑（因为有二阶导数的影子），但其实恰恰这是一道“好题”，因为它充分体现了导数的工具作用，第（2）小题的3种解法中，无论哪种方法都是利用导数作工具，充分研究了函数的性质，特别是单调性，并利用函数的这些性质解决问题。

5.要重视中国古代数学文化

近几年的高考试题增加对中国传统文化进行考查的内容，将中国古代文明作为试题背景材料，体现中国传统文化对人类发展和社会进步的贡献。

这个题目虽然难度不大，但是立意新颖，富有创新精神，特别是巧妙地利用我国优秀的传统文化设计试题，不仅使学生对我国的传统文化有所了解，同时也考查了学生的各种能力，如阅读能力、思维能力、运算能力、数据处理能力等，很好地渗透了数学的核心素养。

声明：本文信息来源于网络，由自主选拔在线团队（微信公众号：zizzsw）排版编辑，如有侵权，请直接联系管理员删除。