全国中学生数学奥林匹克竞赛(决赛)是我国最大规模、最高规格、最具影响力的中学生数学赛事。届时,来自全国各省、自治区、直辖市以及中国香港、中国澳门、俄罗斯、新加坡等代表队的700余名数学英才将齐聚附中,以笔为剑,问鼎逻辑之巅,以题为媒,论道思维宇宙。
推荐阅读:2025年第41届中学生数学竞赛决赛(CMO)全程报道
2025年数学决赛26日开考!官方评分标准与规范答题指南必看
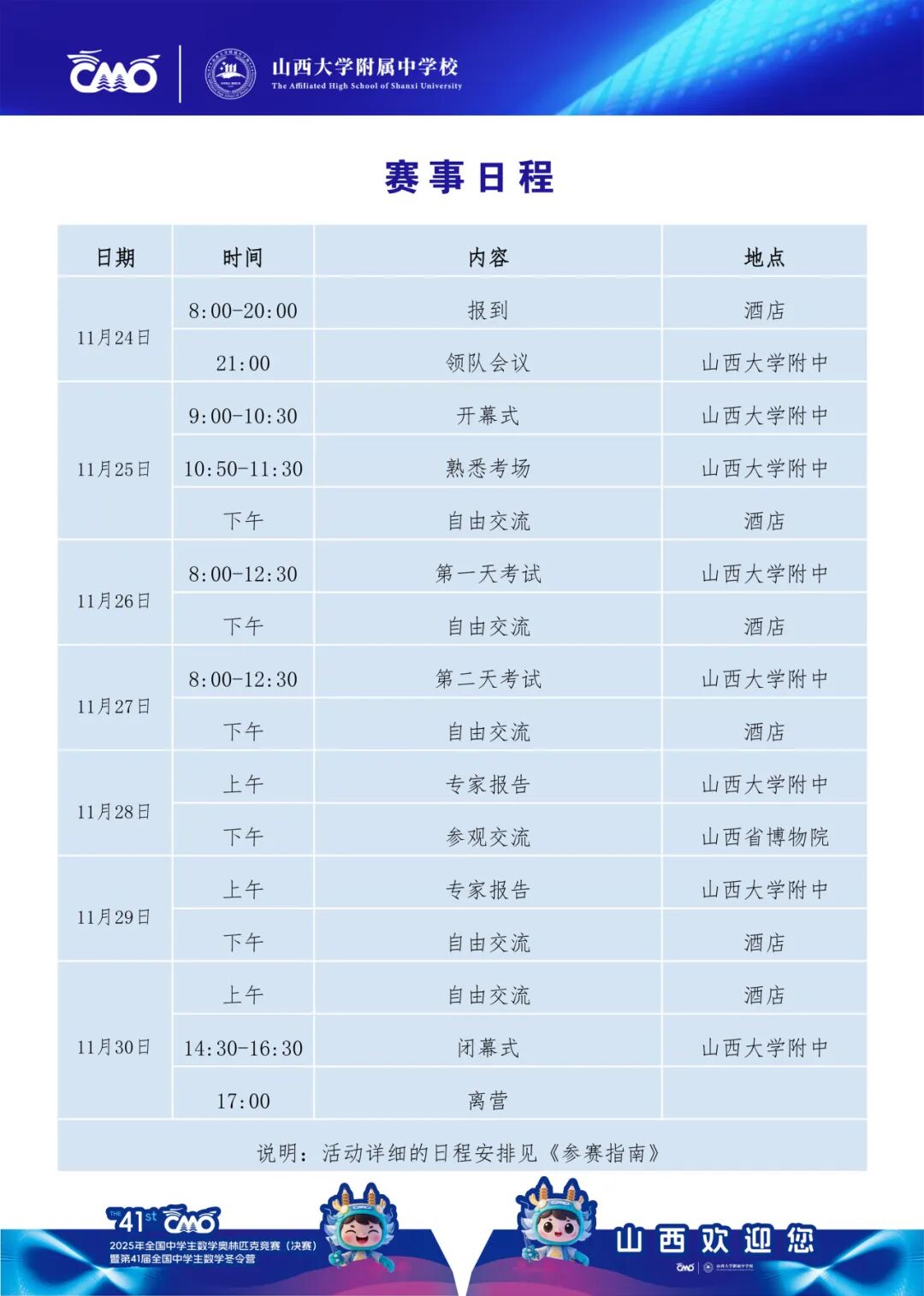
PART.1 行程安排
PART.2 CMO考生须知
CMO试题一共6道,限时四个半小时完成,每题21分,满分共计126分,每道题3分一个得分点。
2024年CMO得分情况:
第一题:代数(容易)351人满分,平均分14.2分;
第二题:几何(中档)416人满分,平均分14分;
第三题:组合(困难)6人满分,平均分0.3分;
第四题:组合几何(容易)293人满分,平均分13.8 分;
第五题:数论(中档)312人满分,平均分11.8分;
第六题:代数(困难)2人满分,平均分1.2分
集训队分数线为87分;金牌分数线为75分;银牌分数线为36分。60人入选国集,金牌218人,银牌306人,铜牌179人!重庆队获得团体第一名,来自上海中学高一的邓乐言获得第一名,并获得唯一满分。
选手只能得知自己的总分,无法知道每道题得了多少分。所以数竞生发起联合投票1238/1329人,希望未来可以公开每道题得分。毕竟大牛娃邓乐言也是要申请复核后,才AK掉CMO。(“AK掉CMO”是竞赛圈的说法,意思是在CMO中拿到满分 。)
2025年IMO金牌选手张恒烨和邓乐言,都曾在CMO中进行过申诉,并成功拿回相应分数。
CMO官方也曾出过《考生答题须知》以规范考生的书写:
CMO考生须知
•一、在每一张答题纸上的指定位置,清楚地写明以下信息:省份、学校全称、姓名、营员号。
• 二、看清答题纸上的题号,每张答题纸上只可以写该题的解答,不要混用。
• 三、卷面应尽可能整洁,如需划去无用的内容,应使用封闭框线将划去分完全框住,并用平行阴影线覆盖。
• 四、答题中需引用定理的结论时,应有正确的格式:
(1)对于冠以人名的定理,应正确叙述人名(Menelaus(梅涅劳斯),Ceva(塞瓦),Ptolemy(托勒密),Simson(西姆松),Fermat(费马),Euler(欧拉),Cauchy(柯西),Chebyshev(切比雪夫),Bezout(裴蜀),De Moivre(棣莫弗),Euclid(欧几里得),Gauss(高斯))(说明:以上为1992和2006年版《数学竞赛大纲》中出现的所有外国人名);《数学竞赛大纲》中提及的定理还包括:余式定理、圆幂定理、多项式的除法定理、因式分解定理、实系数多项式虚根成对定理。
(2)对于《数学竞赛大纲》中未出现的定理,引用时应在定理名称后,将该定理的完整内容叙述在方括号(【】)中。
• 五、答题时应使用规范的文字表述,包括但不限于“若......则......”,“如果......那么......”,“符合题意”(绝不可以写成“合题”)。
PART.3 2024年CMO试题评析
整体来看2024年考试的难度与2023年相仿,仍是1、2、4、5题难度中等,3、6题极难,下面我们来看一下这些题目:

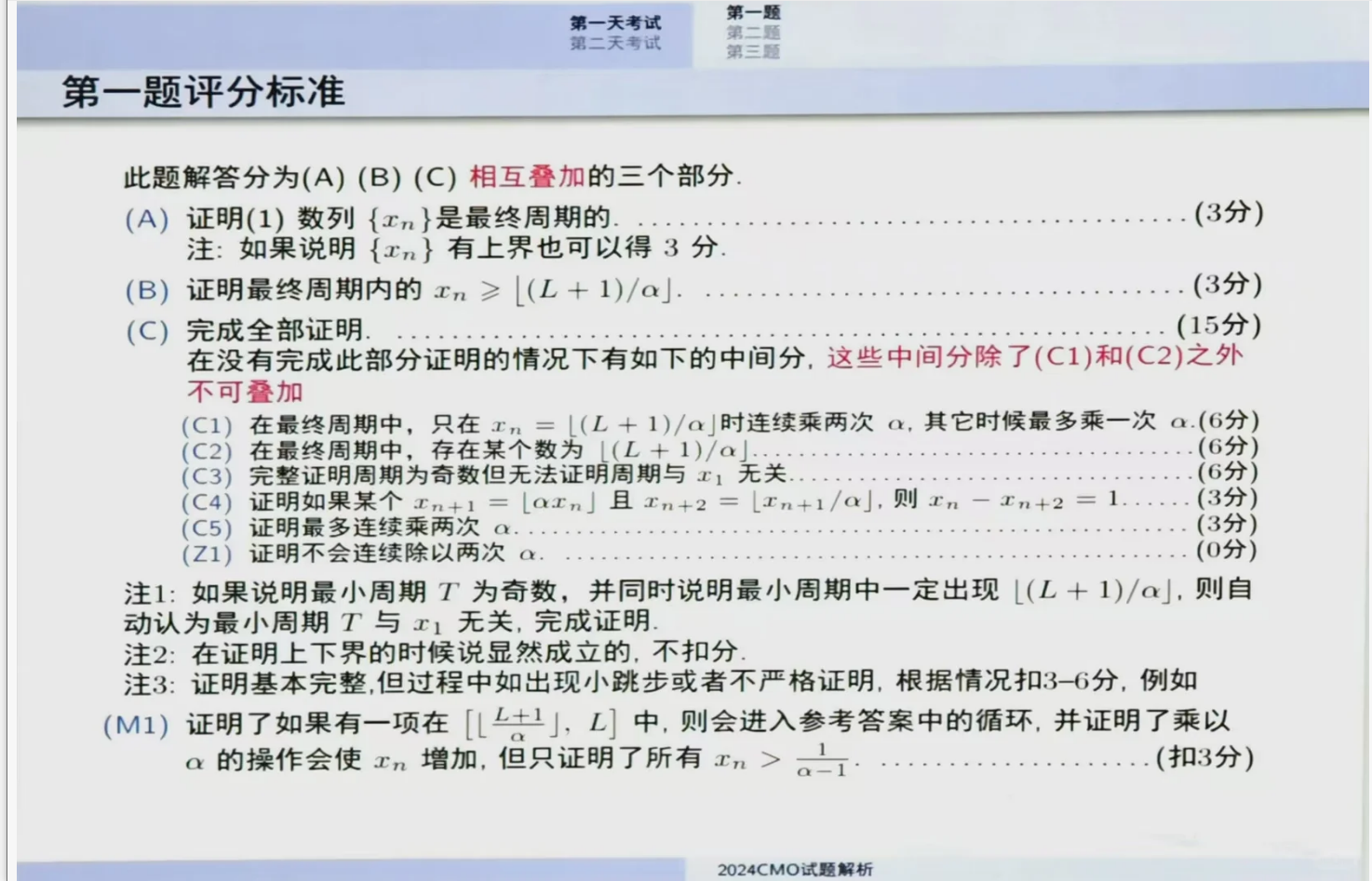
⏩第一题的代数问题延续了二试代数的风格,考查了递推数列的周期性质

该题的切入点较为常规,关键在于寻找数列中相等的两项。
第一问送分;第二问则需要更为细致地研究数列的性质,这类分段递推的数列处理方法较为常见,重点在于如何衔接两类递推关系。
第二类递推的前后应当由第一类递推来连接,合起来呈现出减一的效果,而第一类递推后面接哪一类递推则依赖于与L的距离,因此可以较为容易地找出相等的两项。
本题属于传统的CMO1,难点在于如何准确刻画相等的两项以及书写过程。
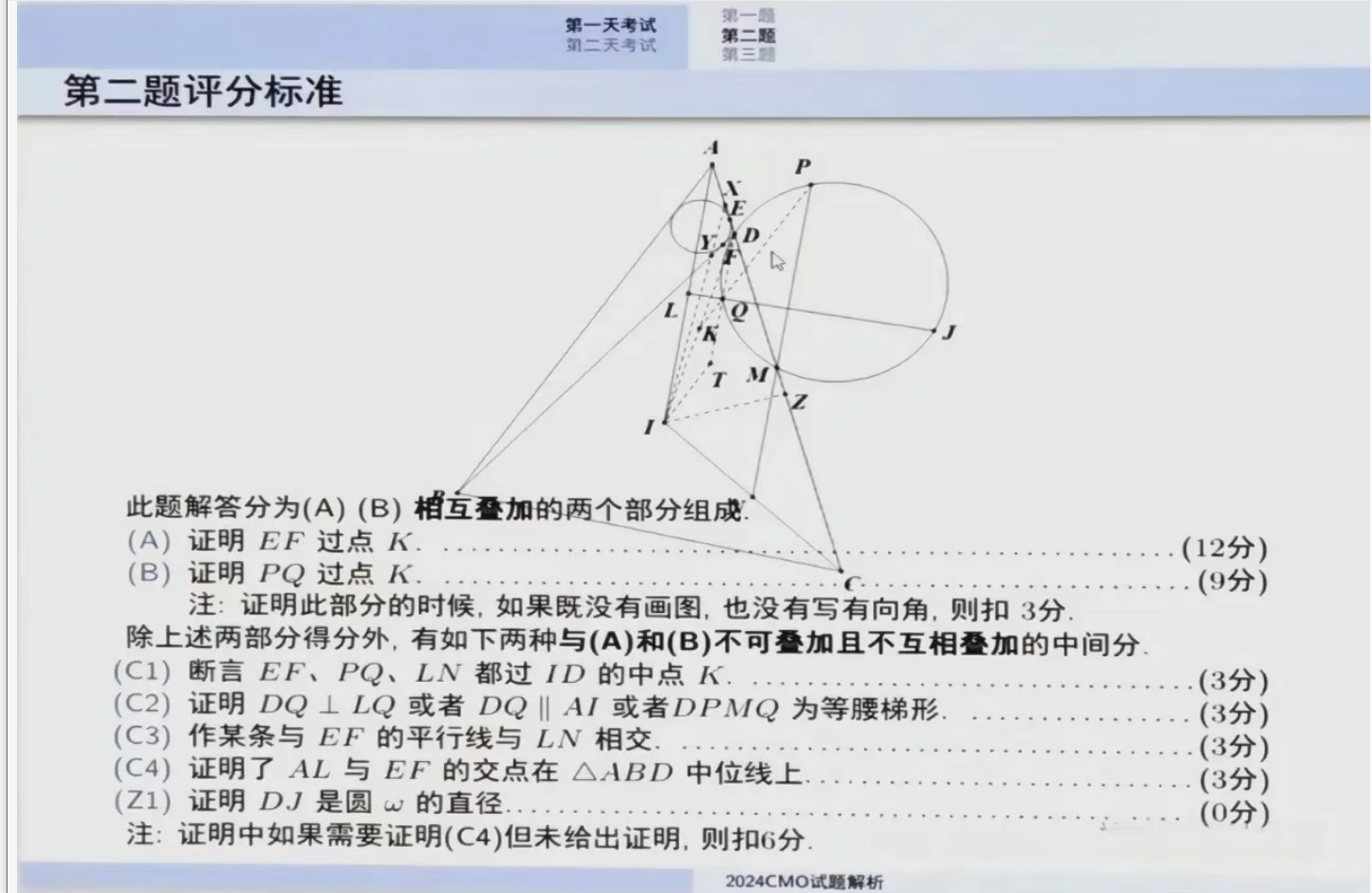
⏩第二题是典型的证明三线共点的平面几何问题

由于LN较为简单,可以分别考虑PQ与LN的交点X以及EF与LN的交点X',从而将问题转化为两个较为简单的图形。
PQ的方向较为明确,倒角容易得到XL=XQ=AD/2。
接下来考虑X',EF的方向同样清晰,因此X'的位置刻画,从而可验证X与X'重合。
本题思路较为常规,无论采用纯几何方法还是计算方法,解题过程都不复杂,属于偏易的CMO2类型。
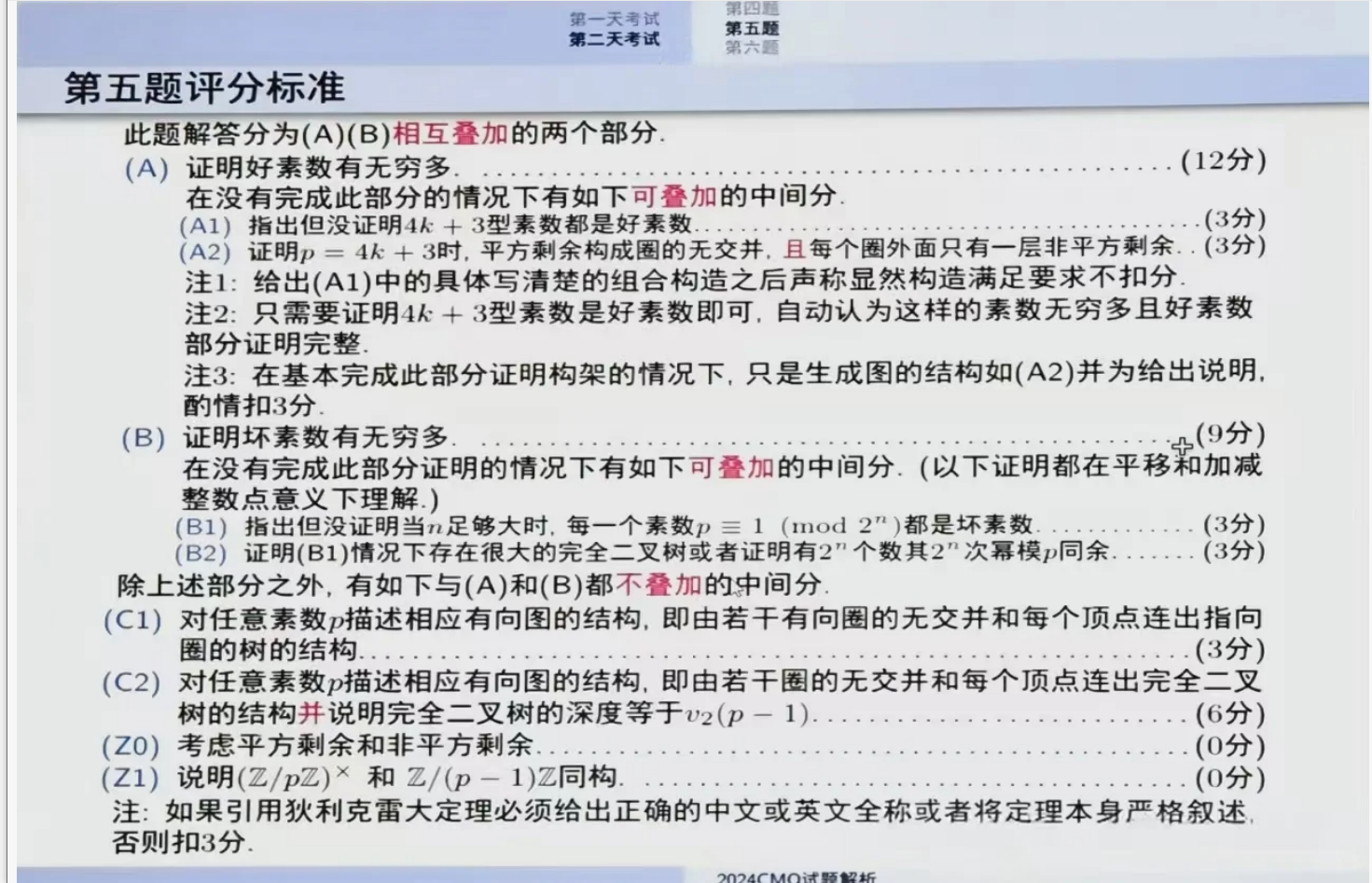
⏩第三题是组合与数论相结合的问题

需证明f(X)的下界,利用极小性可放缩为|X|-1元子集,找出其最小值对应的i,对i求和后算两次可转化为对固定的x关于ai求和的问题,利用数论的知识可得到和的下界。
本题是困难的CMO3,对学生的综合能力以及细节的把控要求都较高。
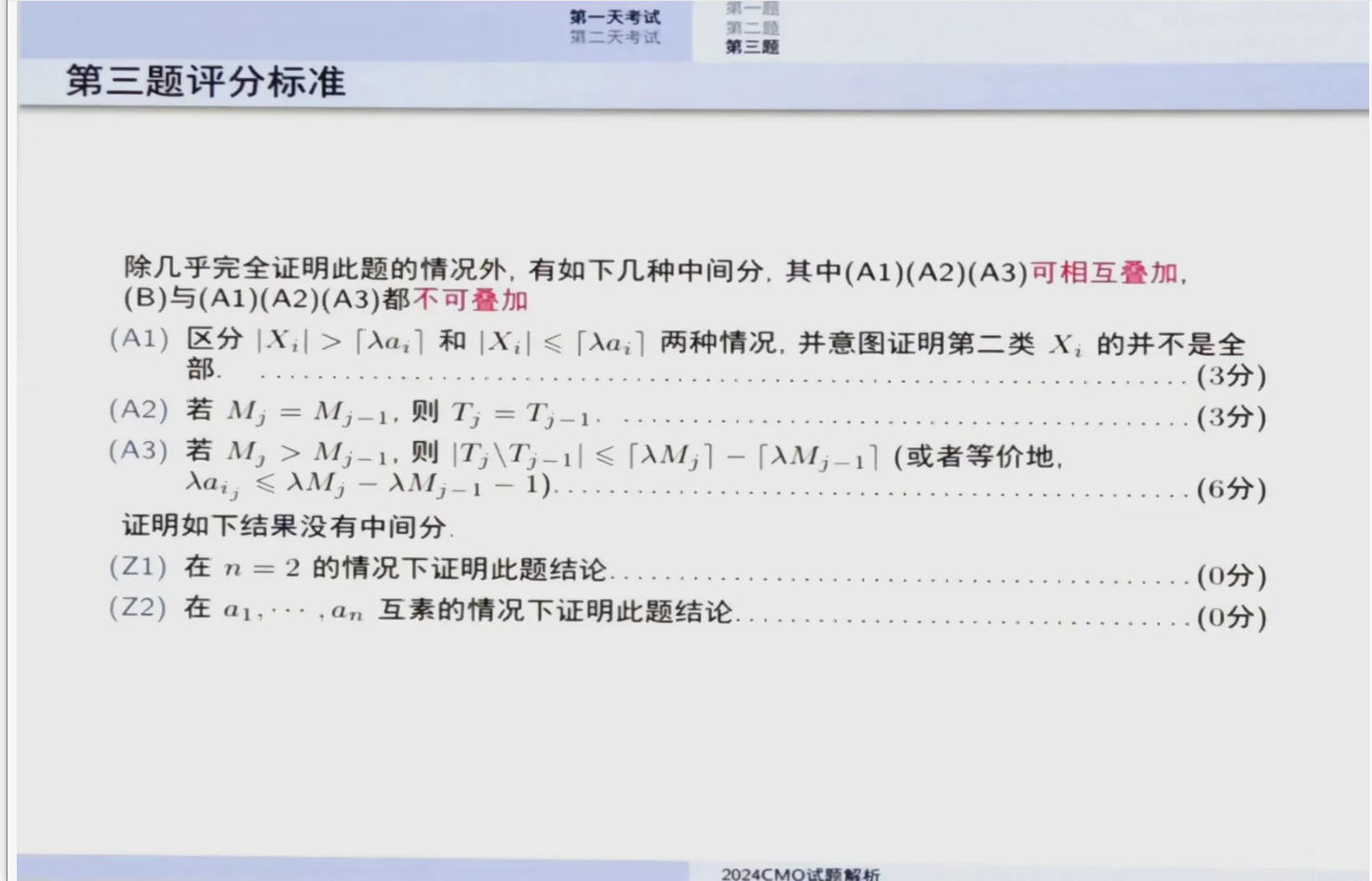
⏩第四题是一个组合几何问题

其关键在于猜测出答案或至少推测出达到答案时点的大致分布。
利用平移不变性可以显著简化问题,在猜出答案后,结合反证法和抽屉原理进行推导以得出矛盾是常规解法。
考场上不少学生在此题卡住,本题属于偏难的CMO4。
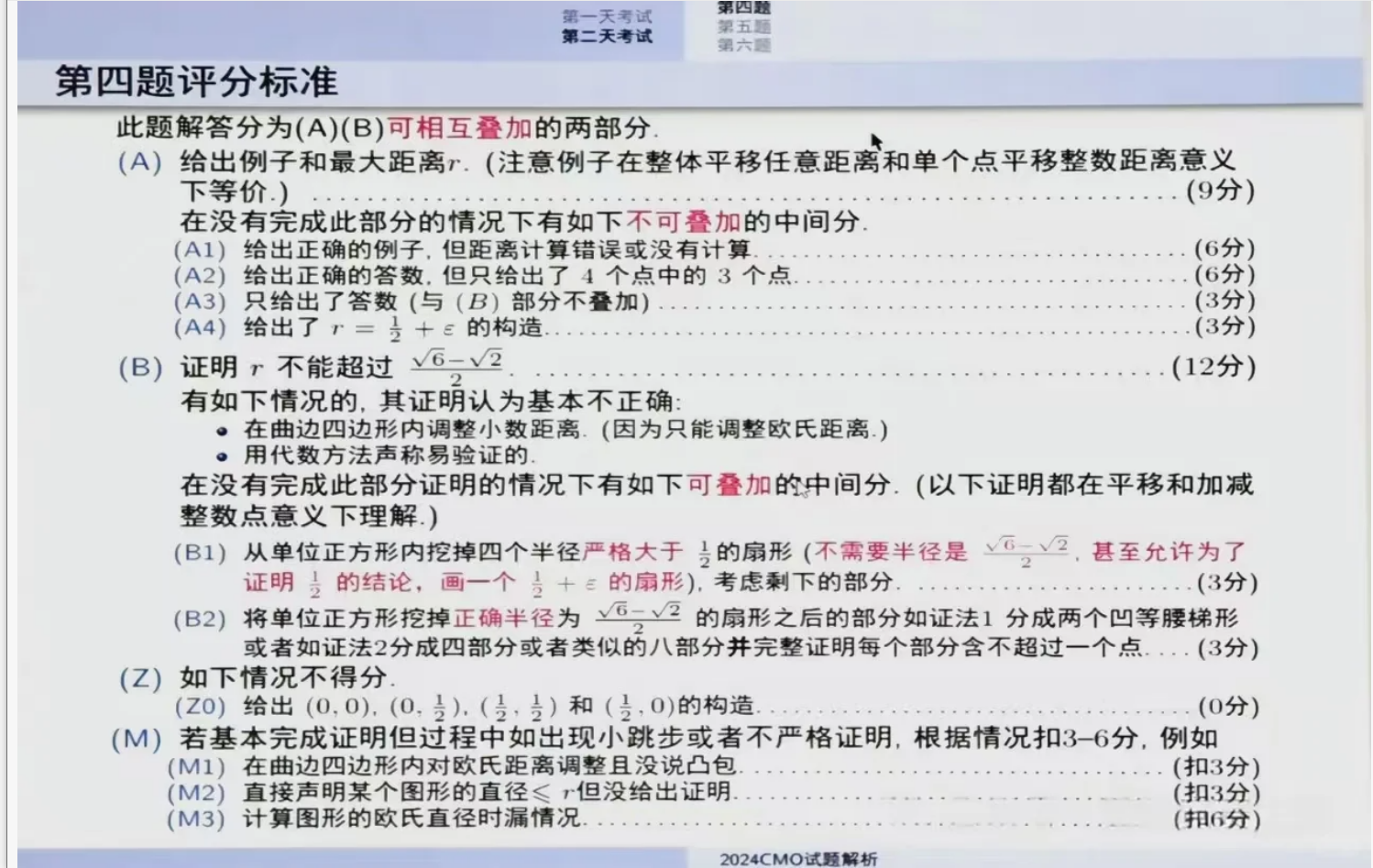
⏩第五题是一道数论问题

其核心在于模意义下a与b=a^2的关系,因此可以借助图论进行分析。
根据关系,b与a、-a相邻,接着对其子节点a、-a作类似分析可以得到二叉树的结构。若2^k||p-1,则形成深度为k的满二叉树,当k充分大时,节点数会变得极多,使得f不存在。而若要使f存在,可以考虑另一种极端情况,即p模4余3,并通过对节点赋值实现。
本题巧妙结合了数论与图论,属于中等难度的CMO5。
⏩第六题是多个约束条件之下研究最大值与最小值差距的代数问题

其中第一问可利用条件猜测答案应满足方程x^3-x^2-x=0,从而构造局部不等式解决。
而第二问需要对第一问的误差作更精细的估计,是非常困难的CMO6。