2026年高中数学奥林匹克竞赛赛制安排一览，如何准备预赛？

2026-02-02 11:22|编辑: 小李老师|阅读: 18

摘要

自主选拔在线依据往年数学竞赛安排，特整理2026年高中数学奥林匹克竞赛赛制安排以及预赛备考指南，一起来看。

2026年全国中学生数学奥林匹克竞赛已进入备战期，自主选拔在线团队梳理了2026年全国中学生数学奥林匹克竞赛完整赛制——从各省预赛、全国高联、CMO决赛，到国家队选拔乃至IMO国际赛场，助你明确方向、精准备战。

2026年高中数学奥林匹克竞赛赛制安排一览，如何准备预赛？

第一阶段：预赛

　　主办方：由各省市自行组织

　　竞赛时间：一般集中在5月-6月。

　　参赛对象：全国在校高中生

　　报名方式：通过所在高中统一报名(个人无法报名)

　　笔试试题难度：略高于高考难度(由各省市自主命题，考试难度等参差不齐)

　　奖项：预赛奖项相当于联赛入场券，部分省市没有预赛，采用名额分配到校形式，由学校组织选拔。

　　2025年各赛区初赛时间：

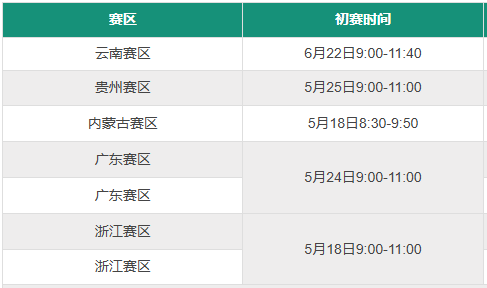
　　福利领取：2026数学竞赛预赛已进入备战期，如何高效备战？领取入口⏭《2012-2025年近15年全国中学生数学竞赛预赛+联赛试题及答案》，提前熟悉出题风格，适应考试节奏。

第二阶段：全国高中数学联赛(高联)

　　主办方：中国数学会

　　竞赛时间：9月第二个周日(一试8:00-9:20，二试9:40-12:30)

　　参赛对象：在预赛中获得名次的在校高中生

　　报名方式：通过所在高中统一报名(个人无法报名哦!)

　　考试形式：笔试试题难度：远大于预赛难度

　　命题要求：全国高中数学联赛(一试)所涉及的知识范围不超出教育部2003年颁布的《普通高中数学课程标准(实验)》中所规定的教学要求和内容，但在方法的要求上有所提高。

　　全国高中数学联赛加试(二试)与中国数学奥林匹克(冬令营)、国际数学奥林匹克接轨，在知识方面有所扩展;适当增加⼀些数学课程标准之外内容。

　　名额：各赛区一等奖名额和冬令营名额由中国数学会竞赛委员会统一分配，按联赛一试和加试总成绩评定。

　　奖项：省一、省二、省三;省一排名靠前同学组成省队参加CMO

　　考试内容：

　　1️⃣一试考试时间共80分钟，总分120分，考察范围不超过高考考察范围，但会对方法有一定要求，比较考验学生的计算能力，共8道填空题(每题8分)+3道大题(分别为16分、20分、20分)。考察函数、数列、不等式、向量复数、排列组合、解析几何、立体几何等模块知识，难度相较于高考而言更大。

　　2️⃣而二试考试时间共170分钟，总分180分，为了更好地与中国数学奥林匹克(冬令营)、国际数学奥林匹克接轨，二试适当增加⼀些数学课程标准之外内容，在知识面方面会有所拓展，共4道大题，考察平面几何、代数、数论、组合数学知识，前两题每题40分，后两题每题50分。

第三阶段：CMO

　　全称为全国中学生数学奥林匹克决赛/全国中学生数学冬令营。2025年数学竞赛决赛由山西大学附属中学举办。

　　主办方：中国数学会

　　竞赛时间：11月

　　参赛对象：

　　各省市省队+中国女子数学奥林匹克竞赛排名靠前的学生。比赛邀请各省、自治区、直辖市在全国高中数学联赛中的优胜者，以及中国香港、中国澳门、俄罗斯、新加坡等代表队近700名学生参加，角逐出全国金银铜牌，全国前60名的选手将入选当年的中国国家集训队，是我国级别最高、规模最大、影响力也最大的中学生数学竞赛。

　　报名方式：通过所在高中统一报名

　　考试形式：笔试

　　试题难度：远大于联赛难度

　　奖项：国一、国二、国三(即金牌、银牌、铜牌);排名前60的同学入选国家集训队，并获得清北等高校保送资格。在强基计划中，竞赛金银牌能够破格入围强基计划或是获得破格资格，不仅如此还能在校考中占据很大的优势。