2024年北京大学中学生数学金秋营于考试结束，北大数学金秋营4个题目，涵盖数论、组合、平面几何、代数，难度介于联赛与决赛之间。自主选拔在线带来北京大学2024年数学金秋营第1题的解析。

北京大学2024年数学金秋营考试试题第1题解析

第1题是一道平面几何题，一道很新颖、也很有难度的题目。此题难度基本在联赛的3，4题及冬令营的1，2题附近。其结构不是很常见，图形优美简洁，题目平中见奇，初看似乎不太难，仔细思考发现很难入手，主要是两组共圆很难用，以及最后的证明结果三点共线也不易转化。本文解答的关键突破口是得到以AN为直径的圆，并发现NK与圆的交点K也在AJ上。解答的难点是对三点共线的描述，先将OAJ共线转化为OAH共线，进而转化为OH⊥NK,后面用圆幂计算基本就是常见套路了。

当然本题的解法还是很多的，也有人用Pascal或雅可比结构来解决本题的。

题目为：

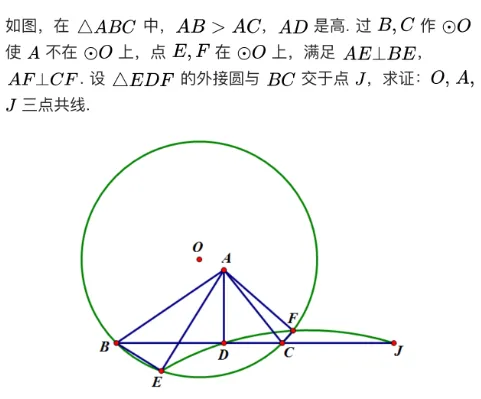
试题解析：

首先，根据题意画出准确的图形，条件都比较“正常”，只需按部就班，按照题目叙述顺序，依次画图即可。其中点E、F为以AB、AC为直径的圆与圆O的交点。准确图形如下：

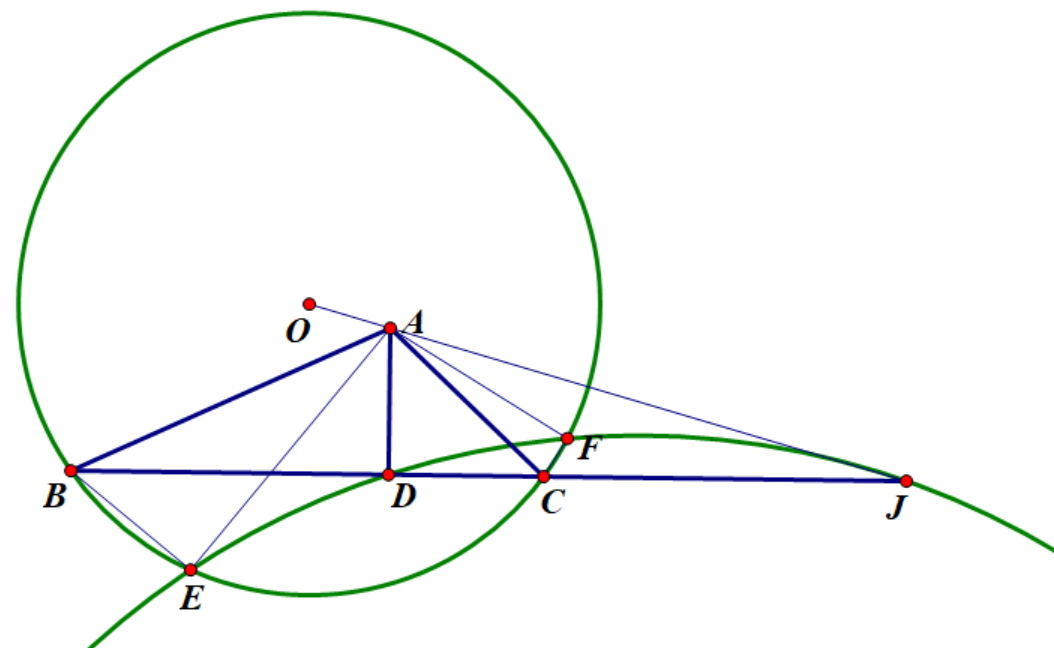
第二步，挖掘图形的基本性质。由垂直，显然ABED,ADCF共圆，点J由EDFJ共圆确定，还有BECF共圆也不好处理。这两个条件很重要，要么得到等角，要么得到比例线段，要么使用三弦定理，感觉都不太好用。

第三步，从结果入手，需证OAJ共线，点A算是基本点，点J满足EDFJ共圆，实在不行就用三弦定理算出DJ。点O也不太描述，最基本的想法就是用BECF中两边中垂线交点来描述。

如何证明共线呢？自然的想法是作BC中点I，则OI⊥BC，从而只需证明：DJ/IJ=AD/OI,

由三弦定理DJ*sin(1-2)

=DE*sin2+DF*sin1,这样就能消去点J，转化为圆上的基本量了，似乎有希望。但是仔细思考一下，发现这些基本量的关系并不好找，点A，O都不好描述，计算量有点大。

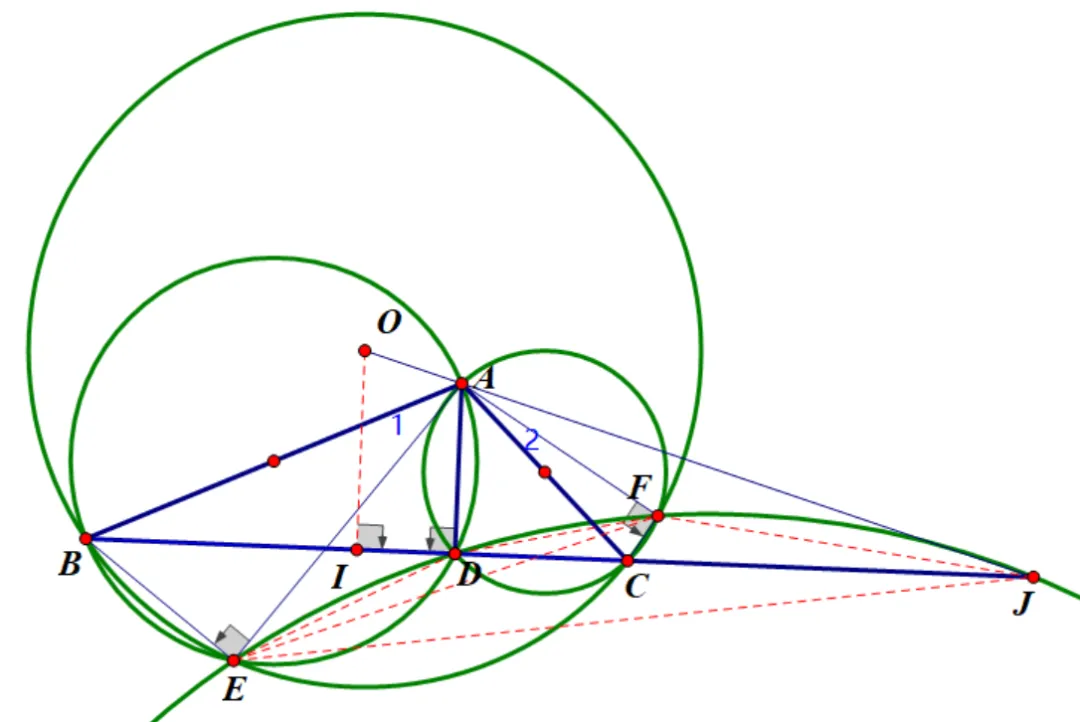
第四步，继续深入挖掘结构的性质，

刚才想通过三弦定理计算消去点J，似乎不太明智，还是继续挖掘点J的性质吧。BECF共圆也很难用，角度看来不好传递，那就用线段，设BC交EF于K，则BK*KC=EK*KF=DK*KJ,

由共圆可以倒角，

∠BAE=∠BDE=180°-∠EDJ

=180°-∠EFJ,从而延长JF交AB于L，

则ALEF共圆，同理AC和JE交点M也在此圆上。进一步，BE和FC交点N也在此圆上，且AN为此圆直径。这个圆应该很有用。进而还会有NL,AE,BC三线共点。还有NK与AJ交点H也在以AN为直径的圆上，这个可以通过相交弦定理证明。

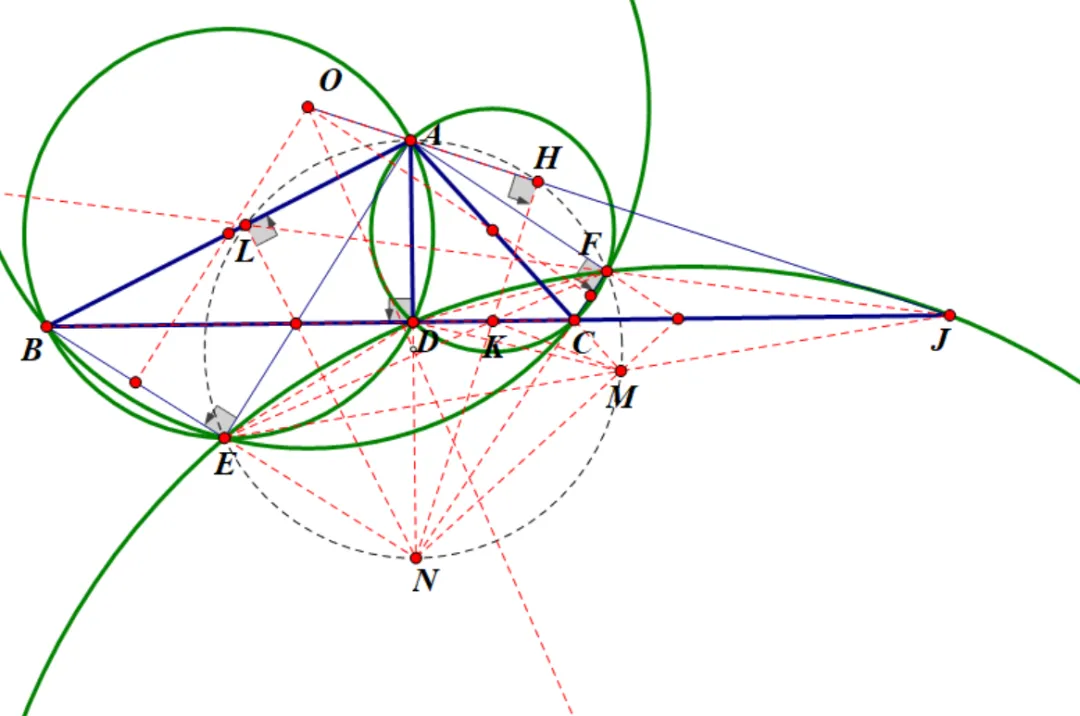
第五步，继续从求证入手，

下面继续从结果分析，OAJ共线很不好证，主要是点O不好描述，用任何两边的中垂线交点都不好用，也可以尝试用EF中垂线，但是还是难有进展。现在AJ上又有H了，所以可以考虑再次消去点J，转而证明OAH共线，证明共线的基本思路是同一角度或者同一比例，发现角度无法传递，比例也不好处理。

经过一段时间的摸索，考虑到AH⊥NH，故可以证明直线OAH⊥NKH，可以从每三个点中选两个来证明（O点必选）即可。证明垂直的思路要么倒角，要么用定差幂线，考虑到O为圆心，这样就可以用定差幂线转化为圆幂来处理。比较好的方式是证OH⊥NK<=>ON^2-OK^2

=HN^2-HK^2<=>NE*NB+KE*KF

=(HN-KH)(HN+KH),

后面用圆幂定理计算一下即可。

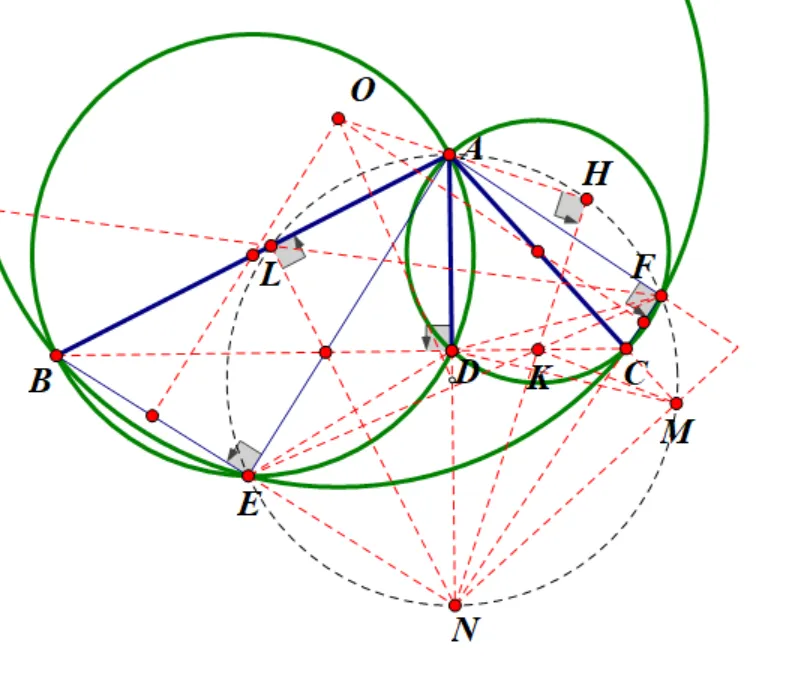
第六步，整理、简化证明，

将上述思路理顺，并把空缺步骤补全，发现点N最好用三圆根心来说，还有点L、M都是不需要的。最后将证明结果整理如下：

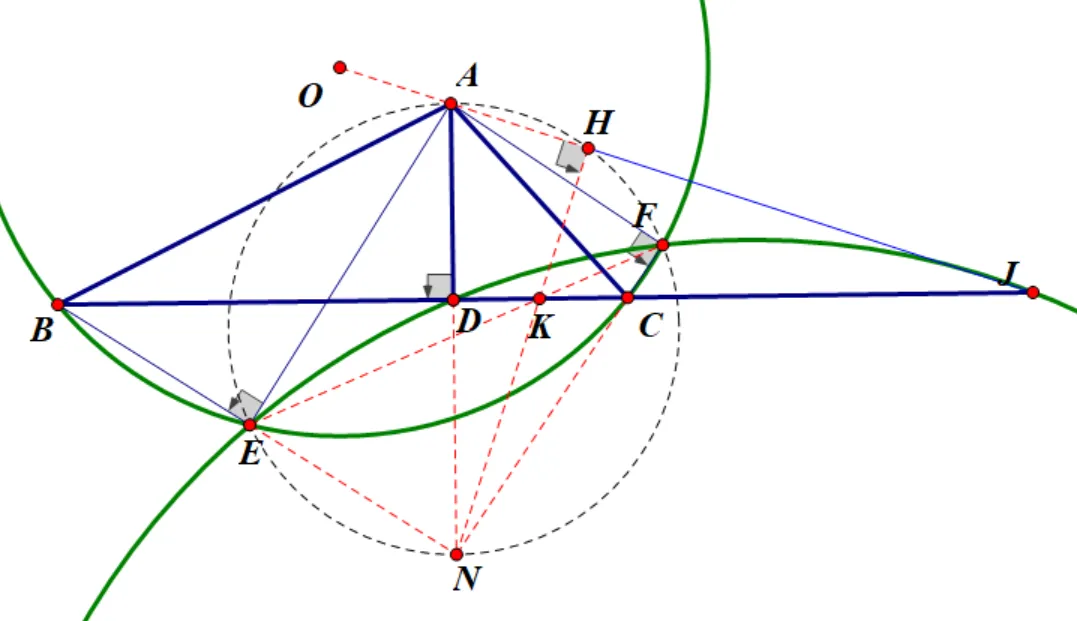
证明：

设圆O半径为R，K为BC，EF交点，

依题意ABED,ADCF,BECF共圆，

由根心定理其三条根轴BE,AD,CF交于一点N，

则AENF在以AN为直径的圆上。

设NK交此圆于H，

则KH*KN=KE*KF=KD*KJ,

故DNJH共圆，

故∠NHJ=∠NDJ=90°,

又∠AHN=90°,故AHJ共线。

则OAJ共线<=>OAH共线<=>OH⊥NK,

<=>ON^2-OK^2=HN^2-HK^2

<=>ON^2-R^2-(OK^2-R^2)=HN^2-HK^2

<=>NE*NB+KE*KF=(HN-KH)(HN+KH)

<=>ND*NA+KN*KH=NK(HN+KH)

<=>NK*HN+NK*KH=NK*HN+NK*KH

显然成立。

温馨提示：

清华、北大金秋营，影响强基报考，考试至关重要！往年考试情况如何？如何备考？自主选拔在线成立【2025清北金秋营交流群】欢迎一起交流~

如果加群失败，可在企业微信联系人中添加青桐老师（微信号：15321584635​）好友，备注：省市-高考年份-选科。